| Числа вида cos(pi/n), n > 3 - иррациональны. Доказательство.
Лемма 1. Существуют многочлены с целыми коэффициентами  и и  степеней, соответственно n и n - 1, для которых степеней, соответственно n и n - 1, для которых
Следствие из теоремы 1. Если cos(a) рационально, то и cos(ka), где k - целое, тоже рационально.
По индукции. База очевидна: при n = 1 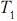 (x)=1 и (x)=1 и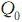 (x)=1. (x)=1.
Переход тоже несложен:
(1)
Лемма доказана. По индукции из формул (1) можно вывести утверждение следующей леммы.
Лемма 2. Старшие коэффициенты многочленов  и и  равны 2^(n-1). равны 2^(n-1).
Поготовка закончена. Теперь для x=cos(pi/n), n > 3 рассмотрим всевозможные n. Предположим, что x рационально.
Если n делится на 4, то противоречие очевидно:
оказывается в силу следствия из леммы 1 рациональным числом.
Если n нечетно, то воспользуемся равенством
Оно означает, что x удовлетворяет уравнению  (x) + 1 = 0. Как известно, рацональные корни многочлена с целыми коэффициентами имеют вид p/q, где p - делитель свободного члена, q - делитель старшего коэффициента. В нашем случае p оказывается сепенью двойки, (x) + 1 = 0. Как известно, рацональные корни многочлена с целыми коэффициентами имеют вид p/q, где p - делитель свободного члена, q - делитель старшего коэффициента. В нашем случае p оказывается сепенью двойки,
а q равно 1, поскольку при нечетном n свободный член многочлена  (x) + 1 равен 1 (свободный член многочлена (x) + 1 равен 1 (свободный член многочлена  можно найти, подставив a = pi/2 в тождество cos(na)= можно найти, подставив a = pi/2 в тождество cos(na)= (cos(a)) ). Значит, x = 1/(2^k)для некого целого неотрицательного k. Осталось вспомнить, что cos(pi/n) > cos(pi/3) = 1/2 - и противоречие получено. (cos(a)) ). Значит, x = 1/(2^k)для некого целого неотрицательного k. Осталось вспомнить, что cos(pi/n) > cos(pi/3) = 1/2 - и противоречие получено. Случай, когда n обладает нечетным делителем m > 3, легко привести к противоречию:
А больше никаких случаев рассматривать не надо - любое натуральное число n > 3 делится на 4 или имеет нечетный делитель, больший числа 3.
| 

